Organic Chemistry Text Book (CHEM 3401 and 3402)
- Home
- Chapter 1: A Review of General ChemistryToggle Dropdown
- 1.1 Introduction to Organic Chemistry
- 1.2 Electrons, Bonds, and Lewis Structures
- 1.3 Identifying Formal Charges
- 1.4 Atomic Orbitals
- 1.5 Valence Bond Theory
- 1.6 Molecular Orbital Theory/Hybridization
- 1.7 VSEPR Theory: Predicting Geometry
- 1.8 Dipole Moments and Molecular Polarity
- 1.9 Intermolecular Forces and Physical Properties
- Problem Set
- Videos for chapter 1
- Chapter 2: Molecular RepresentationsToggle Dropdown
- Chapter 3: Acids and BasesToggle Dropdown
- Chapter 4: Alkanes and CycloalkanesToggle Dropdown
- Chapter 5: Stereochemistry
- Chapter 6: Chemical Reactivity and MechanismsToggle Dropdown
- Chapter 7: Substitution ReactionsToggle Dropdown
- Chapter 8: Addition Reactions of AlkenesToggle Dropdown
- 8.1 Introduction of Addition Reactions
- 8.1 Nomenclature of Alkenes
- 8.2 Hydrohalogenation of Alkenes
- 8.3 Hydration, Hydroboration, and Oxymercuration of Alkenes
- 8.4 Hydrogenation of Alkenes
- 8.5 Halogenation of Alkenes
- 8.6 Dihydroxylation, Epoxidation, and Ozonolysis of Alkenes
- Problem Set
- Chapter 8 Videos
- Chapter 9: AlkynesToggle Dropdown
- Chapter 10: RadicalsToggle Dropdown
- Chapter 11: SynthesisToggle Dropdown
- Problem Sets Organic Chemistry I (CHEM 3401)
- Chapter 12: Alcohols and PhenolsToggle Dropdown
- 12.1 Alcohol Structure
- 12.2 Solubility
- 12.3 Boiling Point & Melting Point
- 12.4 Nomenclature
- 12.5 Alcohol Acidity
- 12.6 Reactions of Alcohols and Phenols
- 12.6.1 Substitution of the Hydroxyl Hydrogen
- 12.6.2 Nucleophilic Substitution of the Hydroxyl Group
- 12.6.3 Elimination Reactions of Alcohols
- 12.6.4 Oxidation Reactions of Alcohols
- 12.6.5 Reactions of Phenols
- 12.7 Practice Problems
- 12.7.1 Alcohol Nomenclature 1
- 12.7.2 Alcohol Nomenclature 2
- 12.7.3 Alcohol Nomenclature 3
- 12.7.4 Formation of Carbonyl Compounds
- 12.7.5 Functional Relationships of Alcohols
- 12.7.6 Reactions of Alcohols & Phenols
- 12.7.7 Alcohol Reactions
- Chapter 13: Ethers and EpoxidesToggle Dropdown
- Chapter 14: Infrared Spectroscopy and Mass SpectrometryToggle Dropdown
- 14.1 Introduction fo Molecular Spectroscopy
- 14.2 Infrared Spectroscopy
- 14.2.1 Introduction
- 14.2.2 Vibrational Spectroscopy
- 14.2.3 Group Frequencies
- 14.2.4 Table of Characteristic IR Frequencies
- 14.3 Mass Spectrometry
- 14.3.1 The Mass Spectrometer
- 14.3.2 Characteristics of Mass Spectra
- 14.3.3 Isotopes
- 14.3.4 Fragmentation Patterns
- 14.3.5 High Resolution Spectra
- 14.3.6 MS Practice Problems
- 14.3.6a Problem 1
- 14.3.6b Problem 2
- 14.3.6c Problem 3
- 14.3.6d Problem 4
- 14.3.6e Problem 5
- 14.3.6f Problem 6
- 14.3.6g Problem 7
- 14.3.6h Problem 8
- Chapter 15: Nuclear Magnetic Resonance Spectroscopy and UV-Visible SpectroscopyToggle Dropdown
- 15.1 Nuclear Magnetic Resonance Spectroscopy
- 15.1.1 Background
- 15.1.2 Proton NMR Spectroscopy
- 15.1.2a Introduction to Proton NMR Spectroscopy
- 15.1.2b Chemical Shift
- 15.1.2c Signal Strength
- 15.1.2d Hydroxyl Proton Exchange and the Influence of Hydrogen Bonding
- 15.1.2e Pi-Electron Functions
- 15.1.2f Solvent Effects
- 15.1.2g Spin-Spin Interactions
- 15.1.2h Examples
- 15.1.3 Carbon NMR Spectroscopy
- 15.1.4 NMR Practice Problems
- 15.1.4a Problem 1
- 15.1.4b Problem 2
- 15.1.4c Problem 3
- 15.1.4d Problem 4
- 15.1.4e Problem 5
- 15.1.4f Problem 6
- 15.1.4g Problem 7
- 15.1.4h Problem 8
- 15.1.4i Problem 9
- 15.1.4j Problem 10
- 15.1.5 Table of Proton NMR Shifts
- 15.1.6 Table of Carbon NMR Shifts
- 15.2 UV-Visible Spectroscopy
- 15.2.1 Background
- 15.2.2 The Electromagnetic Spectrum
- 15.2.3 UV-Visible Absorption Spectra
- 15.2.4 The Importance of Conjugation
- 15.3 Spectroscopy Practice Problems
- Chapter 16: Conjugated Pi Systems and Pericyclic ReactionsToggle Dropdown
- Chapter 17: Aromatic CompoundsToggle Dropdown
- 17.1 Aromaticity
- 17.1.1 Benzene
- 17.1.2 Fused Ring Compounds
- 17.1.3 Other Aromatic Compounds
- 17.1.4 Antiaromaticity
- 17.1.5 Practice Problems
- 17.1.5a Problem 1
- 17.1.5b Problem 2
- 17.2 Reactions of Substituent Groups
- 17.2.1 Oxidation of Alkyl Side-Chains
- 17.2.2 Bromination of Alkyl Side-Chains
- 17.2.3 Reduction of Nitro Groups
- Chapter 17 Videos
- Chapter 18: Aromatic Substitution ReactionsToggle Dropdown
- 18.1 Electrophilic Aromatic Substitution Reactions
- 18.2 Electrophilic Aromatic Substitution Mechanism
- 18.3 Electrophilic Aromatic Substitution Activation/Deactivation and Orientation
- 18.4 Electrophilic Substitution of Disubstituted Benzene Rings
- 18.5 Practice Problems
- 18.5.1 Problem 1
- 18.5.2 Problem 2
- 18.5.3 Problem 3
- 18.5.4 Problem 4
- 18.5.5 Problem 5
- 18.5.6 Problem 6
- 18.5.7 Problem 7
- Chapter 18 Videos
- Chapter 19: Aldehydes and KetonesToggle Dropdown
- 19.1 Nomenclature
- 19.2 Preparation of Aldehydes and Ketones
- 19.3 Properties of Aldehydes and Ketones
- 19.4 Reactions of Aldehydes and Ketones
- 19.4.1 Addition Reactions
- 19.4.1a Hydration
- 19.4.1b Acetal Formation
- 19.4.1c Imine Formation
- 19.4.1d Cyanohydrin Formation
- 19.4.1e Hydride Reduction
- 19.4.1f Addition of Organometallic Reagents
- 19.4.2 Reduction of Aldehydes and Ketones
- 19.4.2a Wolff-Kishner Reduction
- 19.4.2b Clemmensen Reduction
- 19.4.3 Oxidation of Aldehydes and Ketones
- 19.5 Practice Problems
- 19.5.1 Problem 1
- 19.5.2 Problem 2
- 19.5.3 Problem 3
- 19.5.4 Problem 4
- 19.5.5 Problem 5
- 19.5.6 Problem 6
- 19.5.7 Problem 7
- 19.5.8 Problem 8
- 19.5.9 Problem 9
- 19.5.10 Problem 10
- 19.5.11 Problem 11
- 19.5.12 Problem 12
- Chapter 20: Carboxylic Acids and Their DerivativesToggle Dropdown
- 20.1 Nomenclature
- 20.2 Physical Properties
- 20.3 Acidity
- 20.4 Preparation of Carboxylic Acids
- 20.5 Reactions of Carboxylic Acids
- 20.5.1 Salt Formation
- 20.5.2 Substitution of the Hydroxyl Hydrogen
- 20.5.3 Substitution of the Hydroxyl Group
- 20.5.4 Reduction
- 20.5.5 Oxidation
- 20.6 Practice Problems-Carboxylic Acids
- 20.6.1 Nomenclature Practice-1
- 20.6.2 Nomenclature Practice-2
- 20.6.3 Acidity
- 20.6.4 Reactions of Carboxylic Acids
- 20.7 Carboxylic Acid Derivatives
- 20.7.1 Related Derivatives
- 20.7.2 Nomenclature
- 20.7.3 Reactions
- 20.7.3a Acyl Substitution
- 20.7.3b Nitrile Hydrolysis
- 20.7.3c Reductions
- 20.7.3d Reactions with Organometallic Reagents
- 20.7.3e Dehydration of Amides
- 20.7.4 Practice Problems-Carboxylic Acid Derivatives
- 20.7.4a Nomenclature Practice-1
- 20.7.4b Nomenclature Practice-2
- 20.7.4c Carbonyl Compounds
- 20.8 Practice Problems
- 20.8.1 Problem 1
- 20.8.2 Problem 2
- 20.8.3 Problem 3
- 20.8.4 Problem 4
- 20.8.5 Problem 5
- 20.8.6 Problem 6
- Chapter 21: Alpha Carbon Chemistry: Enols and EnolatesToggle Dropdown
- 21.1 Reactions at the Alpha Carbon
- 21.2 Alpha Halogenation of Enols and Enolates
- 21.3 Aldol Reaction
- 21.4 Claisen Condensation
- 21.5 Alkylation at the Alpha Position
- 21.5.1 Enolate Alkylation
- 21.5.2 Dicarbonyl Alkylation
- 21.5.3 Decarboxylation Following Alkylation
- 21.5.4 Conjugate Reactions
- 21.5.4a Michael Reaction
- 21.5.4b Robinson Annulation
- 21.5.4c With Hydrides and Organometallics
- 21.6 Practice Problem
- 21.6.1 Problem 1
- Org Chem II - Problem Sets - Collection (CHEM 3402)
- Problem Set
5.5 Fisher and Other Configurational Notations
Fischer Projection Formulas
The problem of drawing three-dimensional configurations on a two-dimensional surface, such as a piece of paper, has been a long-standing concern of chemists. The wedge and hatched line notations we have been using are effective, but can be troublesome when applied to compounds having many chiral centers. As part of his Nobel Prize-winning research on carbohydrates, the great German chemist Emil Fischer, devised a simple notation that is still widely used. In a Fischer projection drawing, the four bonds to a chiral carbon make a cross with the carbon atom at the intersection of the horizontal and vertical lines. The two horizontal bonds are directed toward the viewer (forward of the stereogenic carbon). The two vertical bonds are directed behind the central carbon (away from the viewer). Since this is not the usual way in which we have viewed such structures, the following diagram shows how a stereogenic carbon positioned in the common two-bonds-in-a-plane orientation ( x–C–y define the reference plane ) is rotated into the Fischer projection orientation (the far right formula). When writing Fischer projection formulas it is important to remember these conventions. Since the vertical bonds extend away from the viewer and the horizontal bonds toward the viewer, a Fischer structure may only be turned by 180º within the plane, thus maintaining this relationship. The structure must not be flipped over or rotated by 90º.
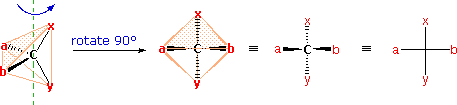
A model of the preceding diagram may be examined by
.
In the above diagram, if x = CO2H, y = CH3, a = H & b = OH, the resulting formula describes (R)-(–)-lactic acid. The mirror-image formula, where x = CO2H, y = CH3, a = OH & b = H, would, of course, represent (S)-(+)-lactic acid.
Using the Fischer projection notation, the stereoisomers of 2-methylamino-1-phenylpropanol are drawn in the following manner. Note that it is customary to set the longest carbon chain as the vertical bond assembly.

The usefulness of this notation to Fischer, in his carbohydrate studies, is evident in the following diagram. There are eight stereoisomers of 2,3,4,5-tetrahydroxypentanal, a group of compounds referred to as the aldopentoses. Since there are three chiral centers in this constitution, we should expect a maximum of 23 stereoisomers. These eight stereoisomers consist of four sets of enantiomers. If the configuration at C-4 is kept constant (R in the examples shown here), the four stereoisomers that result will be diastereomers. Fischer formulas for these isomers, which Fischer designated as the "D"-family, are shown in the diagram. Each of these compounds has an enantiomer, which is a member of the "L"-family so, as expected, there are eight stereoisomers in all. Determining whether a chiral carbon is R or S may seem difficult when using Fischer projections, but it is actually quite simple. If the lowest priority group (often a hydrogen) is on a vertical bond, the configuration is given directly from the relative positions of the three higher-ranked substituents. If the lowest priority group is on a horizontal bond, the positions of the remaining groups give the wrong answer (you are in looking at the configuration from the wrong side), so you simply reverse it.
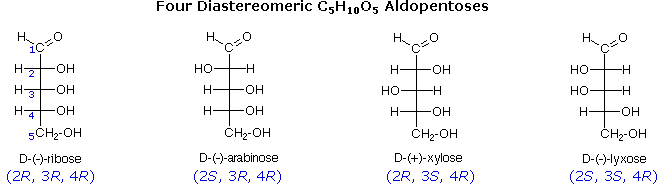
The aldopentose structures drawn above are all diastereomers. A more selective term, epimer, is used to designate diastereomers that differ in configuration at only one chiral center. Thus, ribose and arabinose are epimers at C-2, and arabinose and lyxose are epimers at C-3. However, arabinose and xylose are not epimers, since their configurations differ at both C-2 and C-3.
Formulas Using Other Configurational Notations
Fischer projection formulas are particularly useful for comparing configurational isomers within a family of related chiral compounds, such as the carbohydrates. However, the eclipsed conformations implied by these representations are unrealistic. When describing acyclic compounds incorporating two or more chiral centers, many chemists prefer to write zig-zag line formulas for the primary carbon chain. Here, the zig-zag carbon chain lies in a plane and the absolute or relative configurations at the chiral centers are then designated by wedge or hatched bonds to substituent groups. This is illustrated for D-(-)-ribose and the diastereoisomeric D-tetroses erythrose and threose in the following diagram.
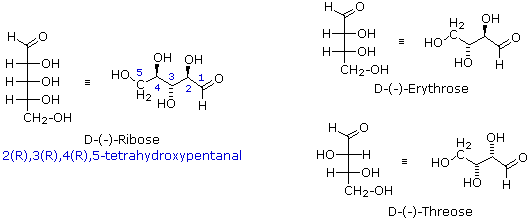
These compounds are all chiral and only one enantiomer is drawn (the D-family member). Many times, however, we must refer to and name diastereoisomers that are racemic or achiral. For example, addition of chlorine to cis-2-butene yields a stereoisomer of 2,3-dichlorobutane different from the one obtained by chlorine addition to trans-2-butene. In cases having two adjacent chiral centers, such as this, the prefixes erythro and threo may be used to designate the relative configuration of the centers. These prefixes, taken from the names of the tetroses erythrose and threose (above), may be applied to racemic compounds, as well as pure enantiomers and meso compounds, as shown in the following diagram. In the commonly used zig-zag drawings substituents may lie on the same side of the carbon chain, a syn orientation, or on opposite sides, an anti orientation. For adjacent (vicinal) substituents this is opposite to their location in a Fischer formula. Thus, the substituents in the erythro isomer have an anti orientation, but are syn in the threo isomer.
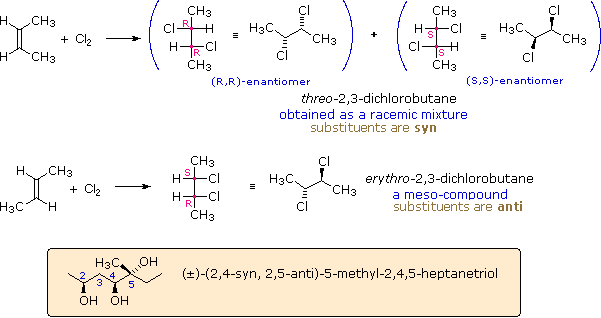
The syn-anti nomenclature may be applied to acyclic compounds having more than two chiral centers, as illustrated by the example in the colored box. The stereogenic center nearest carbon #1 serves as a reference. At sites having two substituents, such as carbon #5, the terms refer to the relative orientation of the highest order substituent, as determined by the C.I.P. sequence rules.
