Organic Chemistry Text Book (CHEM 3401 and 3402)
- Home
-
Chapter 1: A Review of General Chemistry
Toggle Dropdown
- 1.1 Introduction to Organic Chemistry
- 1.2 Electrons, Bonds, and Lewis Structures
- 1.3 Identifying Formal Charges
- 1.4 Atomic Orbitals
- 1.5 Valence Bond Theory
- 1.6 Molecular Orbital Theory/Hybridization
- 1.7 VSEPR Theory: Predicting Geometry
- 1.8 Dipole Moments and Molecular Polarity
- 1.9 Intermolecular Forces and Physical Properties
- Problem Set
- Videos for chapter 1
- Chapter 2: Molecular Representations Toggle Dropdown
- Chapter 3: Acids and Bases Toggle Dropdown
- Chapter 4: Alkanes and Cycloalkanes Toggle Dropdown
- Chapter 5: Stereochemistry Toggle Dropdown
- Chapter 6: Chemical Reactivity and Mechanisms Toggle Dropdown
- Chapter 7: Substitution Reactions Toggle Dropdown
-
Chapter 8: Addition Reactions of Alkenes
Toggle Dropdown
- 8.1 Introduction of Addition Reactions
- 8.1 Nomenclature of Alkenes
- 8.2 Hydrohalogenation of Alkenes
- 8.3 Hydration, Hydroboration, and Oxymercuration of Alkenes
- 8.4 Hydrogenation of Alkenes
- 8.5 Halogenation of Alkenes
- 8.6 Dihydroxylation, Epoxidation, and Ozonolysis of Alkenes
- Problem Set
- Chapter 8 Videos
- Chapter 9: Alkynes Toggle Dropdown
- Chapter 10: Radicals Toggle Dropdown
- Chapter 11: Synthesis Toggle Dropdown
- Problem Sets Organic Chemistry I (CHEM 3401)
-
Chapter 12: Alcohols and Phenols
Toggle Dropdown
- 12.1 Alcohol Structure
- 12.2 Solubility
- 12.3 Boiling Point & Melting Point
- 12.4 Nomenclature
- 12.5 Alcohol Acidity
- 12.6 Reactions of Alcohols and Phenols
- 12.6.1 Substitution of the Hydroxyl Hydrogen
- 12.6.2 Nucleophilic Substitution of the Hydroxyl Group
- 12.6.3 Elimination Reactions of Alcohols
- 12.6.4 Oxidation Reactions of Alcohols
- 12.6.5 Reactions of Phenols
- 12.7 Practice Problems
- 12.7.1 Alcohol Nomenclature 1
- 12.7.2 Alcohol Nomenclature 2
- 12.7.3 Alcohol Nomenclature 3
- 12.7.4 Formation of Carbonyl Compounds
- 12.7.5 Functional Relationships of Alcohols
- 12.7.6 Reactions of Alcohols & Phenols
- 12.7.7 Alcohol Reactions
- Chapter 13: Ethers and Epoxides Toggle Dropdown
-
Chapter 14: Infrared Spectroscopy and Mass Spectrometry
Toggle Dropdown
- 14.1 Introduction fo Molecular Spectroscopy
- 14.2 Infrared Spectroscopy
- 14.2.1 Introduction
- 14.2.2 Vibrational Spectroscopy
- 14.2.3 Group Frequencies
- 14.2.4 Table of Characteristic IR Frequencies
- 14.3 Mass Spectrometry
- 14.3.1 The Mass Spectrometer
- 14.3.2 Characteristics of Mass Spectra
- 14.3.3 Isotopes
- 14.3.4 Fragmentation Patterns
- 14.3.5 High Resolution Spectra
- 14.3.6 MS Practice Problems
- 14.3.6a Problem 1
- 14.3.6b Problem 2
- 14.3.6c Problem 3
- 14.3.6d Problem 4
- 14.3.6e Problem 5
- 14.3.6f Problem 6
- 14.3.6g Problem 7
- 14.3.6h Problem 8
-
Chapter 15: Nuclear Magnetic Resonance Spectroscopy and UV-Visible Spectroscopy
- 15.1 Nuclear Magnetic Resonance Spectroscopy
- 15.1.1 Background
- 15.1.2 Proton NMR Spectroscopy
- 15.1.2a Introduction to Proton NMR Spectroscopy
- 15.1.2b Chemical Shift
- 15.1.2c Signal Strength
- 15.1.2d Hydroxyl Proton Exchange and the Influence of Hydrogen Bonding
- 15.1.2e Pi-Electron Functions
- 15.1.2f Solvent Effects
- 15.1.2g Spin-Spin Interactions
- 15.1.2h Examples
- 15.1.3 Carbon NMR Spectroscopy
- 15.1.4 NMR Practice Problems
- 15.1.4a Problem 1
- 15.1.4b Problem 2
- 15.1.4c Problem 3
- 15.1.4d Problem 4
- 15.1.4e Problem 5
- 15.1.4f Problem 6
- 15.1.4g Problem 7
- 15.1.4h Problem 8
- 15.1.4i Problem 9
- 15.1.4j Problem 10
- 15.1.5 Table of Proton NMR Shifts
- 15.1.6 Table of Carbon NMR Shifts
- 15.2 UV-Visible Spectroscopy
- 15.2.1 Background
- 15.2.2 The Electromagnetic Spectrum
- 15.2.3 UV-Visible Absorption Spectra
- 15.2.4 The Importance of Conjugation
- 15.3 Spectroscopy Practice Problems
- Chapter 16: Conjugated Pi Systems and Pericyclic Reactions Toggle Dropdown
-
Chapter 17: Aromatic Compounds
Toggle Dropdown
- 17.1 Aromaticity
- 17.1.1 Benzene
- 17.1.2 Fused Ring Compounds
- 17.1.3 Other Aromatic Compounds
- 17.1.4 Antiaromaticity
- 17.1.5 Practice Problems
- 17.1.5a Problem 1
- 17.1.5b Problem 2
- 17.2 Reactions of Substituent Groups
- 17.2.1 Oxidation of Alkyl Side-Chains
- 17.2.2 Bromination of Alkyl Side-Chains
- 17.2.3 Reduction of Nitro Groups
- Chapter 17 Videos
-
Chapter 18: Aromatic Substitution Reactions
Toggle Dropdown
- 18.1 Electrophilic Aromatic Substitution Reactions
- 18.2 Electrophilic Aromatic Substitution Mechanism
- 18.3 Electrophilic Aromatic Substitution Activation/Deactivation and Orientation
- 18.4 Electrophilic Substitution of Disubstituted Benzene Rings
- 18.5 Practice Problems
- 18.5.1 Problem 1
- 18.5.2 Problem 2
- 18.5.3 Problem 3
- 18.5.4 Problem 4
- 18.5.5 Problem 5
- 18.5.6 Problem 6
- 18.5.7 Problem 7
- Chapter 18 Videos
-
Chapter 19: Aldehydes and Ketones
Toggle Dropdown
- 19.1 Nomenclature
- 19.2 Preparation of Aldehydes and Ketones
- 19.3 Properties of Aldehydes and Ketones
- 19.4 Reactions of Aldehydes and Ketones
- 19.4.1 Addition Reactions
- 19.4.1a Hydration
- 19.4.1b Acetal Formation
- 19.4.1c Imine Formation
- 19.4.1d Cyanohydrin Formation
- 19.4.1e Hydride Reduction
- 19.4.1f Addition of Organometallic Reagents
- 19.4.2 Reduction of Aldehydes and Ketones
- 19.4.2a Wolff-Kishner Reduction
- 19.4.2b Clemmensen Reduction
- 19.4.3 Oxidation of Aldehydes and Ketones
- 19.5 Practice Problems
- 19.5.1 Problem 1
- 19.5.2 Problem 2
- 19.5.3 Problem 3
- 19.5.4 Problem 4
- 19.5.5 Problem 5
- 19.5.6 Problem 6
- 19.5.7 Problem 7
- 19.5.8 Problem 8
- 19.5.9 Problem 9
- 19.5.10 Problem 10
- 19.5.11 Problem 11
- 19.5.12 Problem 12
-
Chapter 20: Carboxylic Acids and Their Derivatives
Toggle Dropdown
- 20.1 Nomenclature
- 20.2 Physical Properties
- 20.3 Acidity
- 20.4 Preparation of Carboxylic Acids
- 20.5 Reactions of Carboxylic Acids
- 20.5.1 Salt Formation
- 20.5.2 Substitution of the Hydroxyl Hydrogen
- 20.5.3 Substitution of the Hydroxyl Group
- 20.5.4 Reduction
- 20.5.5 Oxidation
- 20.6 Practice Problems-Carboxylic Acids
- 20.6.1 Nomenclature Practice-1
- 20.6.2 Nomenclature Practice-2
- 20.6.3 Acidity
- 20.6.4 Reactions of Carboxylic Acids
- 20.7 Carboxylic Acid Derivatives
- 20.7.1 Related Derivatives
- 20.7.2 Nomenclature
- 20.7.3 Reactions
- 20.7.3a Acyl Substitution
- 20.7.3b Nitrile Hydrolysis
- 20.7.3c Reductions
- 20.7.3d Reactions with Organometallic Reagents
- 20.7.3e Dehydration of Amides
- 20.7.4 Practice Problems-Carboxylic Acid Derivatives
- 20.7.4a Nomenclature Practice-1
- 20.7.4b Nomenclature Practice-2
- 20.7.4c Carbonyl Compounds
- 20.8 Practice Problems
- 20.8.1 Problem 1
- 20.8.2 Problem 2
- 20.8.3 Problem 3
- 20.8.4 Problem 4
- 20.8.5 Problem 5
- 20.8.6 Problem 6
-
Chapter 21: Alpha Carbon Chemistry: Enols and Enolates
Toggle Dropdown
- 21.1 Reactions at the Alpha Carbon
- 21.2 Alpha Halogenation of Enols and Enolates
- 21.3 Aldol Reaction
- 21.4 Claisen Condensation
- 21.5 Alkylation at the Alpha Position
- 21.5.1 Enolate Alkylation
- 21.5.2 Dicarbonyl Alkylation
- 21.5.3 Decarboxylation Following Alkylation
- 21.5.4 Conjugate Reactions
- 21.5.4a Michael Reaction
- 21.5.4b Robinson Annulation
- 21.5.4c With Hydrides and Organometallics
- 21.6 Practice Problem
- 21.6.1 Problem 1
- Org Chem II - Problem Sets - Collection (CHEM 3402)
- Problem Set
15.1.1 Background
Over the past fifty years nuclear magnetic resonance spectroscopy, commonly referred to as nmr, has become the preeminent technique for determining the structure of organic compounds. Of all the spectroscopic methods, it is the only one for which a complete analysis and interpretation of the entire spectrum is normally expected. Although larger amounts of sample are needed than for mass spectroscopy, nmr is non-destructive, and with modern instruments good data may be obtained from samples weighing less than a milligram. To be successful in using nmr as an analytical tool, it is necessary to understand the physical principles on which the methods are based.
The nuclei of many elemental isotopes have a characteristic spin (I). Some nuclei have integral spins (e.g. I = 1, 2, 3 ....), some have fractional spins (e.g. I = 1/2, 3/2, 5/2 ....), and a few have no spin, I = 0 (e.g. 12C, 16O, 32S, ....). Isotopes of particular interest and use to organic chemists are 1H, 13C, 19F and 31P, all of which have I = 1/2. Since the analysis of this spin state is fairly straightforward, our discussion of nmr will be limited to these and other I = 1/2 nuclei.
| For a table of nuclear spin characteristics Click Here. |
|---|
The following features lead to the nmr phenomenon:
|
1. A spinning charge generates a magnetic field, as shown by the animation on the right. |
 |
|
2. In the presence of an external magnetic field (B0), two spin states exist, +1/2and -1/2. |
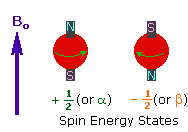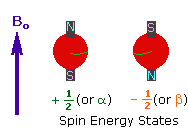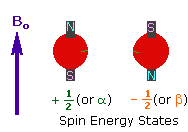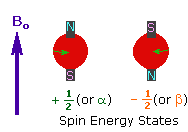 |
|
3. The difference in energy between the two spin states is dependent on the external magnetic field strength, and is always very small. The following diagram illustrates that the two spin states have the same energy when the external field is zero, but diverge as the field increases. At a field equal to Bx a formula for the energy difference is given (remember I = 1/2 and μ is the magnetic moment of the nucleus in the field). |
|
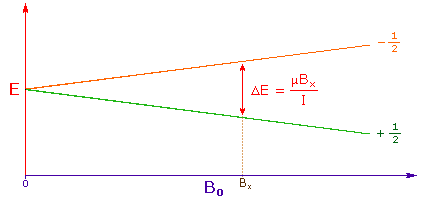 |
|
|---|---|
|
Strong magnetic fields are necessary for nmr spectroscopy. The international unit for magnetic flux is the tesla (T). The earth's magnetic field is not constant, but is approximately 10-4 T at ground level. Modern nmr spectrometers use powerful magnets having fields of 1 to 20 T. Even with these high fields, the energy difference between the two spin states is less than 0.1 cal/mole. To put this in perspective, recall that infrared transitions involve 1 to 10 kcal/mole and electronic transitions are nearly 100 time greater. |
|
|
4. For spin 1/2 nuclei the energy difference between the two spin states at a given magnetic field strength will be proportional to their magnetic moments. For the four common nuclei noted above, the magnetic moments are: 1H μ = 2.7927, 19F μ = 2.6273, 31P μ = 1.1305 & 13C μ = 0.7022. These moments are in nuclear magnetons, which are 5.05078•10-27 JT-1. The following diagram gives the approximate frequencies that correspond to the spin state energy separations for each of these nuclei in an external magnetic field of 2.35 T. The formula in the colored box shows the direct correlation of frequency (energy difference) with magnetic moment (h = Planck's constant = 6.626069•10-34 Js). |
|
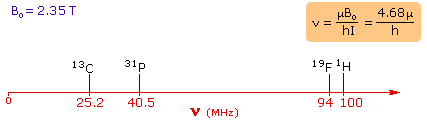 |
|
