Organic Chemistry Text Book (CHEM 3401 and 3402)

Acidity and Basicity

It is useful to begin a discussion of organic chemical reactions with a review of acid-base chemistry and terminology for several reasons. First, acid-base reactions are among the simplest to recognize and understand. Second, some classes of organic compounds have distinctly acidic properties, and some other classes behave as bases, so we need to identify these aspects of their chemistry. Finally, many organic reactions are catalyzed by acids and/or bases, and although such transformations may seem complex, our understanding of how they occur often begins with the functioning of the catalyst.
Organic chemists use two acid-base theories for interpreting and planning their work: the Brønsted theory and the Lewis theory. 

 

Brønsted Theory

According to the Brønsted theory, an acid is a proton donor, and a base is a proton acceptor. In an acid-base reaction, each side of the equilibrium has an acid and a base reactant or product, and these may be neutral species or ions.

 

H-A   +   B:(–)		A:(–)   +   B-H
(acid1)   (base1)		(base2)   (acid2)

 

Structurally related acid-base pairs, such as {H-A and A:^(–)} or {B:^(–) and B-H} are called conjugate pairs. Substances that can serve as both acids and bases, such as water, are termed amphoteric.   

 

H-Cl   +   H2O		Cl:(–)   +   H3O(+)
(acid)     (base)		(base)     (acid)

 

 

H3N:   +   H2O		NH4(+)   +   HO(–)
(base)     (acid)		(acid)       (base)

 

The relative strength of a group of acids (or bases) may be evaluated by measuring the extent of reaction that each group member undergoes with a common base (or acid). Water serves nicely as the common base or acid for such determinations. Thus, for an acid H-A, its strength is proportional to the extent of its reaction with the base water, which is given by the equilibrium constant K_eq.

 

H-A   +   H2O

H3O(+)   +  A:(–)

 

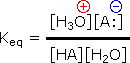Since these studies are generally extrapolated to high dilution, the molar concentration of water (55.5) is constant and may be eliminated from the denominator. The resulting K value is called the acidity constant, K_a. Clearly, strong acids have larger K_a's than do weaker acids. Because of the very large range of acid strengths (greater than 10⁴⁰), a logarithmic scale of acidity (pK_a) is normally employed. Stronger acids have smaller or more negative pK_a values than do weaker acids.  

 

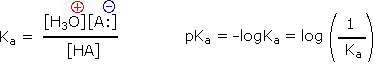
Some useful principles of acid-base reactions are:         • The stronger the acid the weaker its conjugate base; the stronger the base the weaker its conjugate acid.          • Acid-base equilibria always favor the weakest acid and the weakest base.

 

---

Examples of Brønsted Acid-Base Equilibria

 

Acid-Base Reaction				Conjugate Acids	Conjugate Bases	Ka	pKa
HBr   +   H2O		H3O(+)   +   Br(–)		HBr H3O(+)	Br(–) H2O	105	-5
CH3CO2H   +   H2O		H3O(+)   +   CH3CO2(–)		CH3CO2H H3O(+)	CH3CO2(–) H2O	1.77*10-5	4.75
C2H5OH   +   H2O		H3O(+)   +   C2H5O(–)		C2H5OH H3O(+)	C2H5O(–) H2O	10-16	16
NH3   +   H2O		H3O(+)   +   NH2(–)		NH3 H3O(+)	NH2(–) H2O	10-34	34

 

---

 

In all the above examples water acts as a common base. The last example ( NH₃ ) cannot be measured directly in water, since the strongest base that can exist in this solvent is hydroxide ion. Consequently, the value reported here is extrapolated from measurements in much less acidic solvents, such as acetonitrile.

Since many organic reactions either take place in aqueous environments ( living cells ), or are quenched or worked-up in water, it is important to consider how a conjugate acid-base equilibrium mixture changes with pH. A simple relationship known as the Henderson-Hasselbalch equation provides this information.

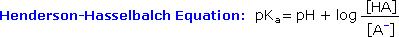
When the pH of an aqueous solution or mixture is equal to the pK_a of an acidic component, the concentrations of the acid and base conjugate forms must be equal ( the log of 1 is 0 ). If the pH is lowered by two or more units relative to the pK_a, the acid concentration will be greater than 99%. On the other hand, if the pH ( relative to pK_a ) is raised by two or more units the conjugate base concentration will be over 99%. Consequently, mixtures of acidic and non-acidic compounds are easily separated by adjusting the pH of the water component in a two phase solvent extraction. 
For example, if a solution of benzoic acid ( pK_a = 4.2 ) in benzyl alcohol ( pK_a = 15 ) is dissolved in ether and shaken with an excess of 0.1 N sodium hydroxide ( pH = 13 ), the acid is completely converted to its water soluble ( ether insoluble ) sodium salt, while the alcohol is unaffected. The ether solution of the alcohol may then be separated from the water layer, and pure alcohol recovered by distillation of the volatile ether solvent. The pH of the water solution of sodium benzoate may then be lowered to 1.0 by addition of hydrochloric acid, at which point pure benzoic acid crystallizes, and may be isolated by filtration.

 

For a discussion of how acidity is influenced by molecular structure Click Here.

Basicity

The basicity of oxygen, nitrogen, sulfur and phosphorus compounds or ions may be treated in an analogous fashion. Thus, we may write base-acid equilibria, which define a K_b and a corresponding pK_b. However, a more common procedure is to report the acidities of the conjugate acids of the bases ( these conjugate acids are often "onium" cations ). The pK_a's reported for bases in this system are proportional to the base strength of the base. A useful rule here is:  pK_a + pK_b = 14. 
We see this relationship in the following two equilibria:

 

Acid-Base Reaction				Conjugate Acids	Conjugate Bases	K	pK
NH3   +   H2O		NH4(+)   +   OH(–)		NH4(+) H2O	NH3 OH(–)	Kb = 1.8*10-5	pKb = 4.74
NH4(+)   +   H2O		H3O(+)   +   NH3		NH4(+) H3O(+)	NH3 H2O	Ka = 5.5*10-10	pKa = 9.25

 

Tables of pK_a values for inorganic and organic acids ( and bases) are available in many reference books, and may be examined here by clicking on the appropriate link: 

Inorganic Acidity Constants
Organic Acidity Constants
Basicity Constants

 

Although it is convenient and informative to express pK_a values for a common solvent system (usually water), there are serious limitations for very strong and very weak acids. Thus acids that are stronger than the hydronium cation, H₃O⁽⁺⁾, and weak acids having conjugate bases stronger than hydroxide anion, OH^(–), cannot be measured directly in water solution. Solvents such as acetic acid, acetonitrile and nitromethane are often used for studying very strong acids. Relative acidity measurements in these solvents may be extrapolated to water. Likewise, very weakly acidic solvents such as DMSO, acetonitrile, toluene, amines and ammonia may be used to study the acidities of very weak acids. For both these groups, the reported pK_a values extrapolated to water are approximate, and many have large uncertainties.  A useful table of pK_a values in DMSO solution has been compiled from the work of F.G. Bordwell, and may be reached by Clicking Here.