Organic Chemistry Text Book (CHEM 3401 and 3402)
- Home
- Chapter 1: A Review of General ChemistryToggle Dropdown
- 1.1 Introduction to Organic Chemistry
- 1.2 Electrons, Bonds, and Lewis Structures
- 1.3 Identifying Formal Charges
- 1.4 Atomic Orbitals
- 1.5 Valence Bond Theory
- 1.6 Molecular Orbital Theory/Hybridization
- 1.7 VSEPR Theory: Predicting Geometry
- 1.8 Dipole Moments and Molecular Polarity
- 1.9 Intermolecular Forces and Physical Properties
- Problem Set
- Videos for chapter 1
- Chapter 2: Molecular RepresentationsToggle Dropdown
- Chapter 3: Acids and BasesToggle Dropdown
- Chapter 4: Alkanes and CycloalkanesToggle Dropdown
- Chapter 5: Stereochemistry
- Chapter 6: Chemical Reactivity and MechanismsToggle Dropdown
- Chapter 7: Substitution ReactionsToggle Dropdown
- Chapter 8: Addition Reactions of AlkenesToggle Dropdown
- 8.1 Introduction of Addition Reactions
- 8.1 Nomenclature of Alkenes
- 8.2 Hydrohalogenation of Alkenes
- 8.3 Hydration, Hydroboration, and Oxymercuration of Alkenes
- 8.4 Hydrogenation of Alkenes
- 8.5 Halogenation of Alkenes
- 8.6 Dihydroxylation, Epoxidation, and Ozonolysis of Alkenes
- Problem Set
- Chapter 8 Videos
- Chapter 9: AlkynesToggle Dropdown
- Chapter 10: RadicalsToggle Dropdown
- Chapter 11: SynthesisToggle Dropdown
- Problem Sets Organic Chemistry I (CHEM 3401)
- Chapter 12: Alcohols and PhenolsToggle Dropdown
- 12.1 Alcohol Structure
- 12.2 Solubility
- 12.3 Boiling Point & Melting Point
- 12.4 Nomenclature
- 12.5 Alcohol Acidity
- 12.6 Reactions of Alcohols and Phenols
- 12.6.1 Substitution of the Hydroxyl Hydrogen
- 12.6.2 Nucleophilic Substitution of the Hydroxyl Group
- 12.6.3 Elimination Reactions of Alcohols
- 12.6.4 Oxidation Reactions of Alcohols
- 12.6.5 Reactions of Phenols
- 12.7 Practice Problems
- 12.7.1 Alcohol Nomenclature 1
- 12.7.2 Alcohol Nomenclature 2
- 12.7.3 Alcohol Nomenclature 3
- 12.7.4 Formation of Carbonyl Compounds
- 12.7.5 Functional Relationships of Alcohols
- 12.7.6 Reactions of Alcohols & Phenols
- 12.7.7 Alcohol Reactions
- Chapter 13: Ethers and EpoxidesToggle Dropdown
- Chapter 14: Infrared Spectroscopy and Mass SpectrometryToggle Dropdown
- 14.1 Introduction fo Molecular Spectroscopy
- 14.2 Infrared Spectroscopy
- 14.2.1 Introduction
- 14.2.2 Vibrational Spectroscopy
- 14.2.3 Group Frequencies
- 14.2.4 Table of Characteristic IR Frequencies
- 14.3 Mass Spectrometry
- 14.3.1 The Mass Spectrometer
- 14.3.2 Characteristics of Mass Spectra
- 14.3.3 Isotopes
- 14.3.4 Fragmentation Patterns
- 14.3.5 High Resolution Spectra
- 14.3.6 MS Practice Problems
- 14.3.6a Problem 1
- 14.3.6b Problem 2
- 14.3.6c Problem 3
- 14.3.6d Problem 4
- 14.3.6e Problem 5
- 14.3.6f Problem 6
- 14.3.6g Problem 7
- 14.3.6h Problem 8
- Chapter 15: Nuclear Magnetic Resonance Spectroscopy and UV-Visible SpectroscopyToggle Dropdown
- 15.1 Nuclear Magnetic Resonance Spectroscopy
- 15.1.1 Background
- 15.1.2 Proton NMR Spectroscopy
- 15.1.2a Introduction to Proton NMR Spectroscopy
- 15.1.2b Chemical Shift
- 15.1.2c Signal Strength
- 15.1.2d Hydroxyl Proton Exchange and the Influence of Hydrogen Bonding
- 15.1.2e Pi-Electron Functions
- 15.1.2f Solvent Effects
- 15.1.2g Spin-Spin Interactions
- 15.1.2h Examples
- 15.1.3 Carbon NMR Spectroscopy
- 15.1.4 NMR Practice Problems
- 15.1.4a Problem 1
- 15.1.4b Problem 2
- 15.1.4c Problem 3
- 15.1.4d Problem 4
- 15.1.4e Problem 5
- 15.1.4f Problem 6
- 15.1.4g Problem 7
- 15.1.4h Problem 8
- 15.1.4i Problem 9
- 15.1.4j Problem 10
- 15.1.5 Table of Proton NMR Shifts
- 15.1.6 Table of Carbon NMR Shifts
- 15.2 UV-Visible Spectroscopy
- 15.2.1 Background
- 15.2.2 The Electromagnetic Spectrum
- 15.2.3 UV-Visible Absorption Spectra
- 15.2.4 The Importance of Conjugation
- 15.3 Spectroscopy Practice Problems
- Chapter 16: Conjugated Pi Systems and Pericyclic ReactionsToggle Dropdown
- Chapter 17: Aromatic CompoundsToggle Dropdown
- 17.1 Aromaticity
- 17.1.1 Benzene
- 17.1.2 Fused Ring Compounds
- 17.1.3 Other Aromatic Compounds
- 17.1.4 Antiaromaticity
- 17.1.5 Practice Problems
- 17.1.5a Problem 1
- 17.1.5b Problem 2
- 17.2 Reactions of Substituent Groups
- 17.2.1 Oxidation of Alkyl Side-Chains
- 17.2.2 Bromination of Alkyl Side-Chains
- 17.2.3 Reduction of Nitro Groups
- Chapter 17 Videos
- Chapter 18: Aromatic Substitution ReactionsToggle Dropdown
- 18.1 Electrophilic Aromatic Substitution Reactions
- 18.2 Electrophilic Aromatic Substitution Mechanism
- 18.3 Electrophilic Aromatic Substitution Activation/Deactivation and Orientation
- 18.4 Electrophilic Substitution of Disubstituted Benzene Rings
- 18.5 Practice Problems
- 18.5.1 Problem 1
- 18.5.2 Problem 2
- 18.5.3 Problem 3
- 18.5.4 Problem 4
- 18.5.5 Problem 5
- 18.5.6 Problem 6
- 18.5.7 Problem 7
- Chapter 18 Videos
- Chapter 19: Aldehydes and KetonesToggle Dropdown
- 19.1 Nomenclature
- 19.2 Preparation of Aldehydes and Ketones
- 19.3 Properties of Aldehydes and Ketones
- 19.4 Reactions of Aldehydes and Ketones
- 19.4.1 Addition Reactions
- 19.4.1a Hydration
- 19.4.1b Acetal Formation
- 19.4.1c Imine Formation
- 19.4.1d Cyanohydrin Formation
- 19.4.1e Hydride Reduction
- 19.4.1f Addition of Organometallic Reagents
- 19.4.2 Reduction of Aldehydes and Ketones
- 19.4.2a Wolff-Kishner Reduction
- 19.4.2b Clemmensen Reduction
- 19.4.3 Oxidation of Aldehydes and Ketones
- 19.5 Practice Problems
- 19.5.1 Problem 1
- 19.5.2 Problem 2
- 19.5.3 Problem 3
- 19.5.4 Problem 4
- 19.5.5 Problem 5
- 19.5.6 Problem 6
- 19.5.7 Problem 7
- 19.5.8 Problem 8
- 19.5.9 Problem 9
- 19.5.10 Problem 10
- 19.5.11 Problem 11
- 19.5.12 Problem 12
- Chapter 20: Carboxylic Acids and Their DerivativesToggle Dropdown
- 20.1 Nomenclature
- 20.2 Physical Properties
- 20.3 Acidity
- 20.4 Preparation of Carboxylic Acids
- 20.5 Reactions of Carboxylic Acids
- 20.5.1 Salt Formation
- 20.5.2 Substitution of the Hydroxyl Hydrogen
- 20.5.3 Substitution of the Hydroxyl Group
- 20.5.4 Reduction
- 20.5.5 Oxidation
- 20.6 Practice Problems-Carboxylic Acids
- 20.6.1 Nomenclature Practice-1
- 20.6.2 Nomenclature Practice-2
- 20.6.3 Acidity
- 20.6.4 Reactions of Carboxylic Acids
- 20.7 Carboxylic Acid Derivatives
- 20.7.1 Related Derivatives
- 20.7.2 Nomenclature
- 20.7.3 Reactions
- 20.7.3a Acyl Substitution
- 20.7.3b Nitrile Hydrolysis
- 20.7.3c Reductions
- 20.7.3d Reactions with Organometallic Reagents
- 20.7.3e Dehydration of Amides
- 20.7.4 Practice Problems-Carboxylic Acid Derivatives
- 20.7.4a Nomenclature Practice-1
- 20.7.4b Nomenclature Practice-2
- 20.7.4c Carbonyl Compounds
- 20.8 Practice Problems
- 20.8.1 Problem 1
- 20.8.2 Problem 2
- 20.8.3 Problem 3
- 20.8.4 Problem 4
- 20.8.5 Problem 5
- 20.8.6 Problem 6
- Chapter 21: Alpha Carbon Chemistry: Enols and EnolatesToggle Dropdown
- 21.1 Reactions at the Alpha Carbon
- 21.2 Alpha Halogenation of Enols and Enolates
- 21.3 Aldol Reaction
- 21.4 Claisen Condensation
- 21.5 Alkylation at the Alpha Position
- 21.5.1 Enolate Alkylation
- 21.5.2 Dicarbonyl Alkylation
- 21.5.3 Decarboxylation Following Alkylation
- 21.5.4 Conjugate Reactions
- 21.5.4a Michael Reaction
- 21.5.4b Robinson Annulation
- 21.5.4c With Hydrides and Organometallics
- 21.6 Practice Problem
- 21.6.1 Problem 1
- Org Chem II - Problem Sets - Collection (CHEM 3402)
- Problem Set
5.3 Enantiomers and Diastereomers
Chirality and Symmetry
All objects may be classified with respect to a property we call chirality (from the Greek cheir meaning hand). A chiral object is not identical in all respects (i.e. superimposable) with its mirror image. An achiral object is identical with (superimposable on) its mirror image. Chiral objects have a "handedness", for example, golf clubs, scissors, shoes and a corkscrew. Thus, one can buy right or left-handed golf clubs and scissors. Likewise, gloves and shoes come in pairs, a right and a left. Achiral objects do not have a handedness, for example, a baseball bat (no writing or logos on it), a plain round ball, a pencil, a T-shirt and a nail. The chirality of an object is related to its symmetry, and to this end it is useful to recognize certain symmetry elements that may be associated with a given object. A symmetry element is a plane, a line or a point in or through an object, about which a rotation or reflection leaves the object in an orientation indistinguishable from the original. Some examples of symmetry elements are shown below.
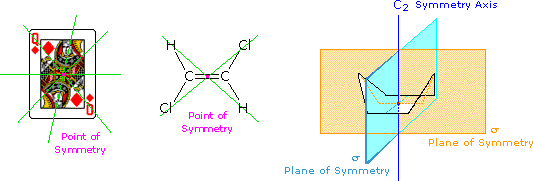
The face playing card provides an example of a center or point of symmetry. Starting from such a point, a line drawn in any direction encounters the same structural features as the opposite (180º) line. Four random lines of this kind are shown in green. An example of a molecular configuration having a point of symmetry is (E)-1,2-dichloroethene. Another way of describing a point of symmetry is to note that any point in the object is reproduced by reflection through the center onto the other side. In these two cases the point of symmetry is colored magenta.
The boat conformation of cyclohexane shows an axis of symmetry (labeled C2 here) and two intersecting planes of symmetry (labeled σ). The notation for a symmetry axis is Cn, where n is an integer chosen so that rotation about the axis by 360/nº returns the object to a position indistinguishable from where it started. In this case the rotation is by 180º, so n=2. A plane of symmetry divides the object in such a way that the points on one side of the plane are equivalent to the points on the other side by reflection through the plane. In addition to the point of symmetry noted earlier, (E)-1,2-dichloroethene also has a plane of symmetry (the plane defined by the six atoms), and a C2 axis, passing through the center perpendicular to the plane. The existence of a reflective symmetry element (a point or plane of symmetry) is sufficient to assure that the object having that element is achiral. Chiral objects, therefore, do not have any reflective symmetry elements, but may have rotational symmetry axes, since these elements do not require reflection to operate. In addition to the chiral vs achiral distinction, there are two other terms often used to refer to the symmetry of an object. These are:
(i) Dissymmetry: The absence of reflective symmetry elements. All dissymmetric objects are chiral.
(ii) Asymmetry: The absence of all symmetry elements. All asymmetric objects are chiral.
Enantiomorphism
A consideration of the chirality of molecular configurations explains the curious stereoisomerism observed for lactic acid, carvone and a multitude of other organic compounds. Tetravalent carbons have a tetrahedral configuration. If all four substituent groups are the same, as in methane or tetrachloromethane, the configuration is that of a highly symmetric "regular tetrahedron". A regular tetrahedron has six planes of symmetry and seven symmetry axes (four C3 & three C2) and is, of course, achiral. Examples of these Axes and Planes are found on George Hart's VRML site.
If one of the carbon substituents is different from the other three, the degree of symmetry is lowered to a C3 axis and three planes of symmetry, but the configuration remains achiral. The tetrahedral configuration in such compounds is no longer regular, since bond lengths and bond angles change as the bonded atoms or groups change. Further substitution may reduce the symmetry even more, but as long as two of the four substituents are the same there is always a plane of symmetry that bisects the angle linking those substituents, so these configurations are also achiral.
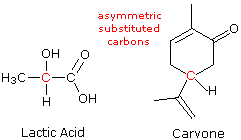 A carbon atom that is bonded to four different atoms or groups loses all symmetry, and is often referred to as an asymmetric carbon. The configuration of such a molecular unit is chiral, and the structure may exist in either a right-handed configuration or a left-handed configuration (one the mirror image of the other). This type of configurational stereoisomerism is termed enantiomorphism, and the non-identical, mirror-image pair of stereoisomers that result are called enantiomers. The structural formulas of lactic acid and carvone are drawn on the right with the asymmetric carbon colored red. Consequently, we expect, and find, these compounds to exist as pairs of enantiomers. The presence of a single asymmetrically substituted carbon atom in a molecule is sufficient to render the whole configuration chiral, and modern terminology refers to such asymmetric (or dissymmetric) groupings as chiral centers. Most of the chiral centers we shall discuss are asymmetric carbon atoms, but it should be recognized that other tetrahedral or pyramidal atoms may become chiral centers if appropriately substituted. When more than one chiral center is present in a molecular structure, care must be taken to analyze their relationship before concluding that a specific molecular configuration is chiral or achiral. This aspect of stereoisomerism will be treated later.
A carbon atom that is bonded to four different atoms or groups loses all symmetry, and is often referred to as an asymmetric carbon. The configuration of such a molecular unit is chiral, and the structure may exist in either a right-handed configuration or a left-handed configuration (one the mirror image of the other). This type of configurational stereoisomerism is termed enantiomorphism, and the non-identical, mirror-image pair of stereoisomers that result are called enantiomers. The structural formulas of lactic acid and carvone are drawn on the right with the asymmetric carbon colored red. Consequently, we expect, and find, these compounds to exist as pairs of enantiomers. The presence of a single asymmetrically substituted carbon atom in a molecule is sufficient to render the whole configuration chiral, and modern terminology refers to such asymmetric (or dissymmetric) groupings as chiral centers. Most of the chiral centers we shall discuss are asymmetric carbon atoms, but it should be recognized that other tetrahedral or pyramidal atoms may become chiral centers if appropriately substituted. When more than one chiral center is present in a molecular structure, care must be taken to analyze their relationship before concluding that a specific molecular configuration is chiral or achiral. This aspect of stereoisomerism will be treated later.
The identity or non-identity of mirror-image configurations of some substituted carbons may be examined as interactive models by .
A useful first step in examining structural formulas to determine whether stereoisomers may exist is to identify all stereogenic elements. A stereogenic element is a center, axis or plane that is a focus of stereoisomerism, such that an interchange of two groups attached to this feature leads to a stereoisomer. Stereogenic elements may be chiral or achiral. An asymmetric carbon is often a chiral stereogenic center, since interchanging any two substituent groups converts one enantiomer to the other. However, care must be taken when evaluating bridged structures in which bridgehead carbons are asymmetric. This caveat will be illustrated by Clicking Here.
Alkenes having two different groups on each double bond carbon (e.g. abC=Cab) constitute an achiral stereogenic element, since interchanging substituents at one of the carbons changes the cis/trans configuration of the double bond. Chiral stereogenic axes or planes may be present in a molecular configuration, as in the case of allenes, but these are less common than chiral centers and will not be discussed here.
| For additional information about chiral axes and planes Click Here. |
Structural formulas for eight organic compounds are displayed in the frame below. Some of these structures are chiral and some are achiral. First, try to identify all chiral stereogenic centers. Formulas having no chiral centers are necessarily achiral. Formulas having one chiral center are always chiral; and if two or more chiral centers are present in a given structure it is likely to be chiral, but in special cases, to be discussed later, may be achiral. Once you have made your selections of chiral centers, check them by pressing the "Show Stereogenic Centers" button. The chiral centers will be identified by red dots.
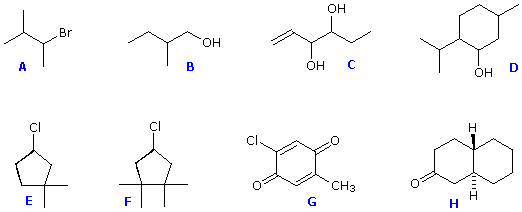
Structures F and G are achiral. The former has a plane of symmetry passing through the chlorine atom and bisecting the opposite carbon-carbon bond. The similar structure of compound Edoes not have such a symmetry plane, and the carbon bonded to the chlorine is a chiral center (the two ring segments connecting this carbon are not identical). Structure G is essentially flat. All the carbons except that of the methyl group are sp2 hybridized, and therefore trigonal-planar in configuration. Compounds C, D & H have more than one chiral center, and are also chiral. Remember, all chiral structures may exist as a pair of enantiomers. Other configurational stereoisomers are possible if more than one stereogenic center is present in a structure.
